Jiancong Li's Blog
0%

C++ 关于加法溢出的判断

Posted on Edited on In

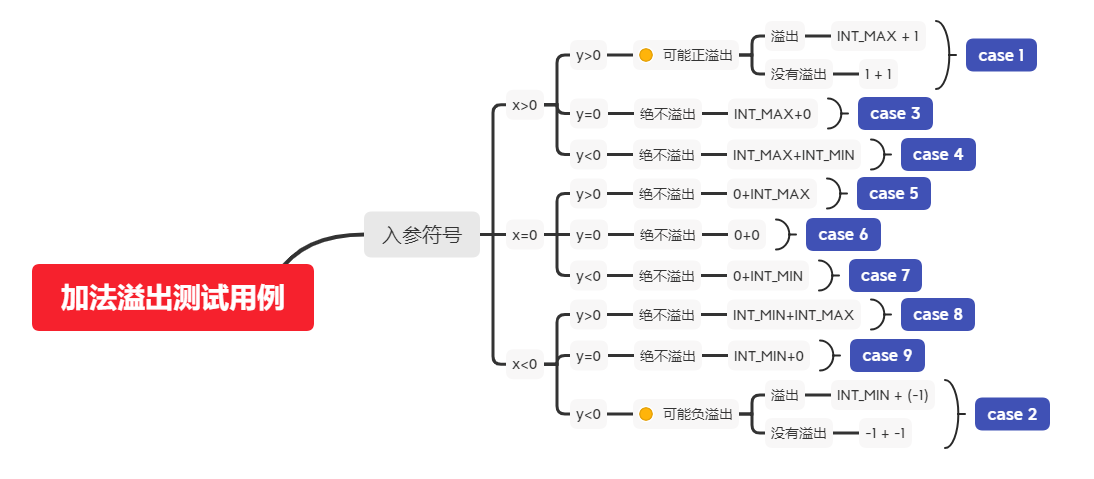
分析问题

首先我们知道整型是由有符号和无符号整型所组成。由于有符号整型的判断包含了无符号整型的计算，所以我们现在先讨论有符号整型。

1592040132570

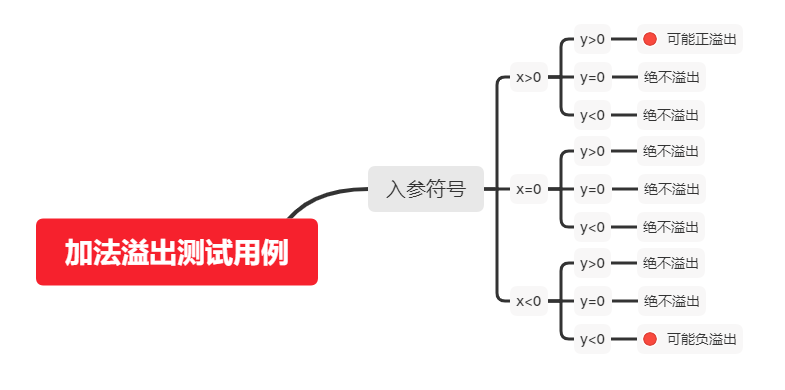
有符号整型的加法包括以下几种情况：

1592042113575

由上图我们可以知道我们只用考虑两个操作数拥有相同符号的情况就行了。我们显而易见的可以知道，两数相加的结果一定大于任一操作数，写出以下函数。

1
2
3
4
5
6
7
8
9
10
/// 溢出了返回true，否则返回false
bool is_plus_overflow(int x, int y) {
  if (x > 0 && y > 0) {
    /// 计算正溢出的情况
    int result = x + y;
    return result < x;
  }

  return false;
}

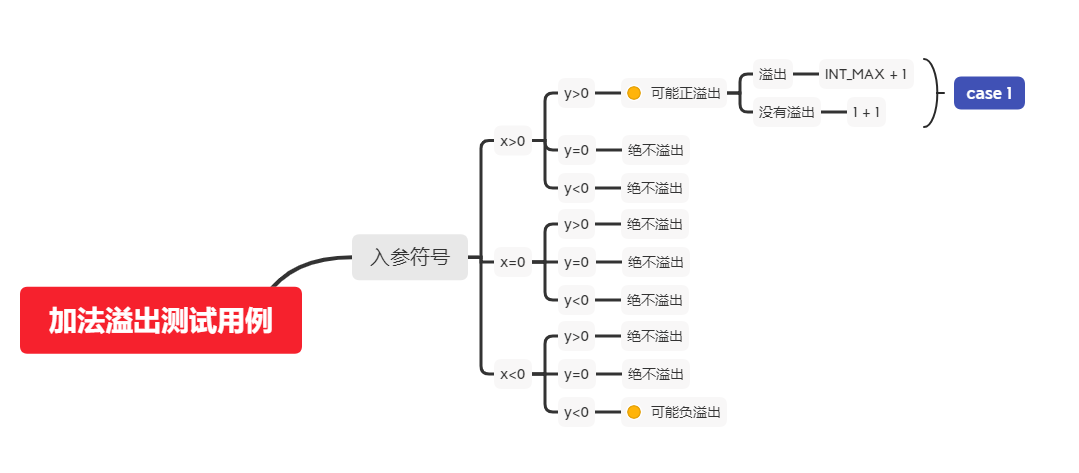
接下来为了测试这个函数能否正确运行，我们添加如下测试用例：case 1.

1592044663011

完整验证程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <cassert>
#include <iostream>
#include <limits>

/// 溢出了返回true，否则返回false
bool is_plus_overflow(int x, int y) {
  if (x > 0 && y > 0) {
    /// 计算正溢出的情况
    int result = x + y;
    return result < x;
  }

  return false;
}

int main() {
  /// 获取int类型的最大值和最小值
  const int int_min = std::numeric_limits<int>::min();
  const int int_max = std::numeric_limits<int>::max();

  /// case 1
  assert(!is_plus_overflow(1, 1));  ///< 没有溢出
  assert(is_plus_overflow(int_max, 1));  ///< 溢出了
}

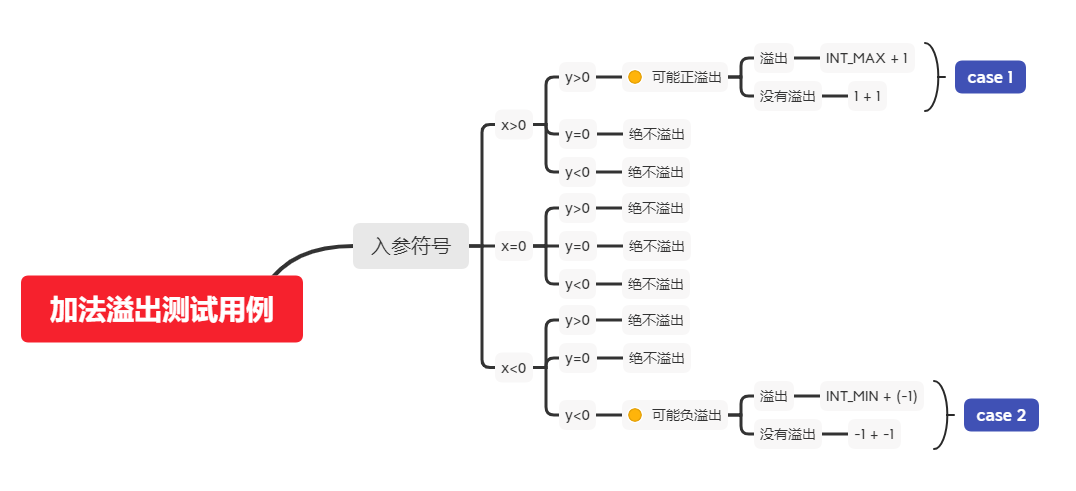
接下来考虑两数都为负数，判断负溢出的情况，同样我们知道两负数相加结果一定小于任一操作数, 对函数加以补充，并添加两个测试用例：case 2.

1592044894101

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <cassert>
#include <iostream>
#include <limits>

/// 溢出了返回true，否则返回false
bool is_plus_overflow(int x, int y) {
  if (x > 0 && y > 0) {
    /// 计算正溢出的情况
    int result = x + y;
    return result < x;
  } else if (x < 0 && y < 0) {
    /// 计算负溢出的情况
    int result = x + y;
    return result > x;
  }

  return false;
}

int main() {
  /// 获取int类型的最大值和最小值
  const int int_min = std::numeric_limits<int>::min();
  const int int_max = std::numeric_limits<int>::max();

  /// case 1
  assert(!is_plus_overflow(1, 1));  ///< 没有溢出
  assert(is_plus_overflow(int_max, 1));  ///< 溢出了

  /// case 2
  assert(!is_plus_overflow(-1, -1));  ///< 没有溢出
  assert(is_plus_overflow(int_min, -1));  ///< 溢出了
}

当上面的程序顺利执行完毕后我们可以继续往下看。接着我们能不能使用模板来扩展到其他类型的加法.

当然可以我们只需要把int换为模板参数T就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<typename T>
bool is_plus_overflow_t(T x, T y) {
  if (x > 0 && y > 0) {
    /// 计算正溢出的情况
    T result = x + y;
    return result < x;
  } else if (x < 0 && y < 0) {
    /// 计算负溢出的情况
    T result = x + y;
    return result > x;
  }

  return false;
}

接下来我们为模板函数添加上类型限定和静态编译检查。然后同样使用测试用例:case 1 和 case 2 来测试以下这个模板函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <cassert>
#include <iostream>
#include <limits>

template <typename T1, typename T2>
bool is_plus_overflow_t(const T1& x, const T2& y) {
  /// 编译时判断两个入参的类型是否一致
  static_assert(std::is_same<T1, T2>::value,
                "is_plus_overflow need same type!");
  /// 编译时判断两个入参类型都为整数类型
  static_assert(std::is_integral<T1>::value,
                "is_plus_overflow need integral type!");

  T1 result = x + y;
  if (x > 0 && y > 0) {
    return result < x;
  } else if (x < 0 && y < 0) {
    return result > x;
  } else {
    return false;
  }
}

int main() {
  /// 获取int类型的最大值和最小值
  constexpr auto int_min = std::numeric_limits<int>::min();
  constexpr auto int_max = std::numeric_limits<int>::max();

  /// case 1
  assert(!is_plus_overflow_t(1, 1));  ///< 没有溢出
  assert(is_plus_overflow_t(int_max, 1));  ///< 溢出了

  /// case 2
  assert(!is_plus_overflow_t(-1, -1));  ///< 没有溢出
  assert(is_plus_overflow_t(int_min, -1));  ///< 溢出了
}

接下来添加上详细的测试用例就大功告成了。

1592130012130

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <cassert>
#include <iostream>
#include <limits>

template <typename T1, typename T2>
bool is_plus_overflow_t(const T1& x, const T2& y) {
  /// 编译时判断两个入参的类型是否一致
  static_assert(std::is_same<T1, T2>::value,
                "is_plus_overflow need same type!");
  /// 编译时判断两个入参类型都为整数类型
  static_assert(std::is_integral<T1>::value,
                "is_plus_overflow need integral type!");

  T1 result = x + y;
    if (x > 0 && y > 0) {
      return result < x;
    } else if (x < 0 && y < 0) {
      return result > x;
    } else {
      return false;
    }
}

int main() {
  /// 获取int类型的最大值和最小值
  constexpr auto min_num = std::numeric_limits<int>::min();
  constexpr auto max_num = std::numeric_limits<int>::max();

  /// case 1
  assert(!is_plus_overflow_t(1, 1));       ///< 没有溢出
  assert(is_plus_overflow_t(max_num, 1));  ///< 溢出了

  /// case 2
  assert(!is_plus_overflow_t(-1, -1));      ///< 没有溢出
  assert(is_plus_overflow_t(min_num, -1));  ///< 溢出了

  /// case 3
  assert(!is_plus_overflow_t(max_num, 0));
  /// case 4
  assert(!is_plus_overflow_t(max_num, min_num));
  /// case 5
  assert(!is_plus_overflow_t(0, max_num));
  /// case 6
  assert(!is_plus_overflow_t(0, 0));
  /// case 7
  assert(!is_plus_overflow_t(0, min_num));
  /// case 8
  assert(!is_plus_overflow_t(min_num, max_num));
  /// case 9
  assert(!is_plus_overflow_t(min_num, 0));
}

后记

这个函数也可以用作检查减法是否溢出，只需要对第二个入参求相反数即可。但需要注意一个情况。

就是int值的负数个数(- 2^31)是比正数个数(2^31 - 1)多一个的, 所以在转化为相反数的时候可能在函数入参时出现溢出，导致计算没有溢出。

1
2
3
4
5
6
7
int x = 2;
int y = 1;
is_plus_overflow_t(x, y);	/// 正确：等价与计算 2-1 表达式会不会溢出

x = 2;
y = INT_MIN;
is_plus_overflow_t(x, -y);	/// 错误：当y等于int的最小值的时候，无法求其相反数，会直接溢出